3 Leggi di Newton e Vettori
TEORIA NEWTON
Prima Legge di Newton
(Legge dell’Inerzia)
Enunciato
Un corpo rimane in stato di quiete o di moto rettilineo uniforme fino a quando una forza esterna non agisce su di esso.
concetti chiave
- Inerzia: tendenza di un corpo a mantenere il suo stato di moto o quiete.
- Se la somma delle forze applicate a un corpo è zero, il corpo non cambia stato.

Un oggetto fermo su un piano rimane immobile finché non viene spinto...
In pratica il vaso resta lì... finché non arriva il gatto a buttarlo giù.

Un veicolo in movimento continua a muoversi anche se mettiamo in folle (quindi senza accelerare e frenare). Poiché esistono le forze di attrito (aria/ruote) il veicolo rallenterà fino a fermarsi.

Se l'autobus frena bruscamente, le persone tendono a saltare in avanti (osservando dall'esterno tendono a mantenere la stessa velocità).
Seconda Legge di Newton
(Legge Fondamentale della Dinamica)
Enunciato
La forza risultante che agisce su un corpo è uguale al prodotto della sua massa e della sua accelerazione.
$$ \overrightarrow{F} = m \cdot \overrightarrow{a} $$
concetti chiave
- La forza è proporzionale alla massa (oggetti più pesanti richiedono più forza per essere accelerati).
- L'accelerazione è inversamente proporzionale alla massa, a parità di forza applicata (oggetti più leggeri accelerano più velocemente).

Una macchina pesante accelera lentamente e necessita di tanta forza prodotta dal motore (motore con più cilindrata e maggiori consumi).
I vigili del fuoco nel bellunese devono tener conto anche del carico d'acqua per affrontare salite e tornanti per arrivare in tempo nei paesi e frazioni.

Per fermare un auto normale nello stesso spazio bastano freni meno potenti di un camion (più massa) o auto da corsa (più variazione di velocità = più accelerazione).

Far prendere velocità (lanciare) un sassolino è facile, spostare un masso è difficile.
PS: l'immagine non è reale!!!
Terza Legge di Newton
(Azione - reazione)
Enunciato
Ad ogni azione corrisponde una reazione uguale e contraria.
$$ \overrightarrow{F_{AB}} = \overrightarrow{F_{BA}} $$
concetti chiave
- Le forze si manifestano in coppie: una forza di azione e una di reazione.
- Le due forze agiscono su corpi diversi e non si annullano.

Quando camminiamo, spingiamo il terreno indietro, e il terreno ci spinge avanti.

Le eliche spingono in giù l'aria, l'aria il drone verso l'alto.

In un incidente si generano grandi forze (muro/auto o auto/auto) che fermano la macchina in breve tempo. Questa forza viene assorbita dalla deformazione della macchina, così sul corpo umano arriva in forma minore.
TEORIA VETTORI
Vettoriale e scalare
Grandezza scalare
- Una grandezza scalare è definita da un valore numerico e un’unità di misura.
- Esempi: massa (kg), tempo (s), temperatura (°K), energia (J).
Grandezza Vettoriale
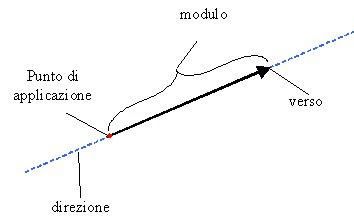
- Una grandezza vettoriale è definita da:
- Modulo: il valore numerico e unità di misura.
- Direzione: la linea lungo la quale la grandezza agisce.
- Verso: L'orientamento lungo la direzione.
- Esempi: Forza (𝑁), velocità (𝑚/𝑠), accelerazione (𝑚/𝑠2).
- La rappresentazione grafica è una freccia, il simbolo è la lettera con una freccia sopra di essa.
Operazioni con i vettori
Concetto
- A differenza del normale calcolo, i vettori devono essere disegnati in giusta scala (la lunghezza è data dal modulo) per poter applicare poi i giusti calcoli matematici.
- Posso scomporli utilizzando le regole geometriche e trigonometriche (le vedremo solo in parte).
- Posso calcolare il modulo a parte e trovare poi il punto di applicazione.
- Attenzione: ci sono 3 tipi di moltiplicazione che danno risultati completamente diversi!
Somma di vettori
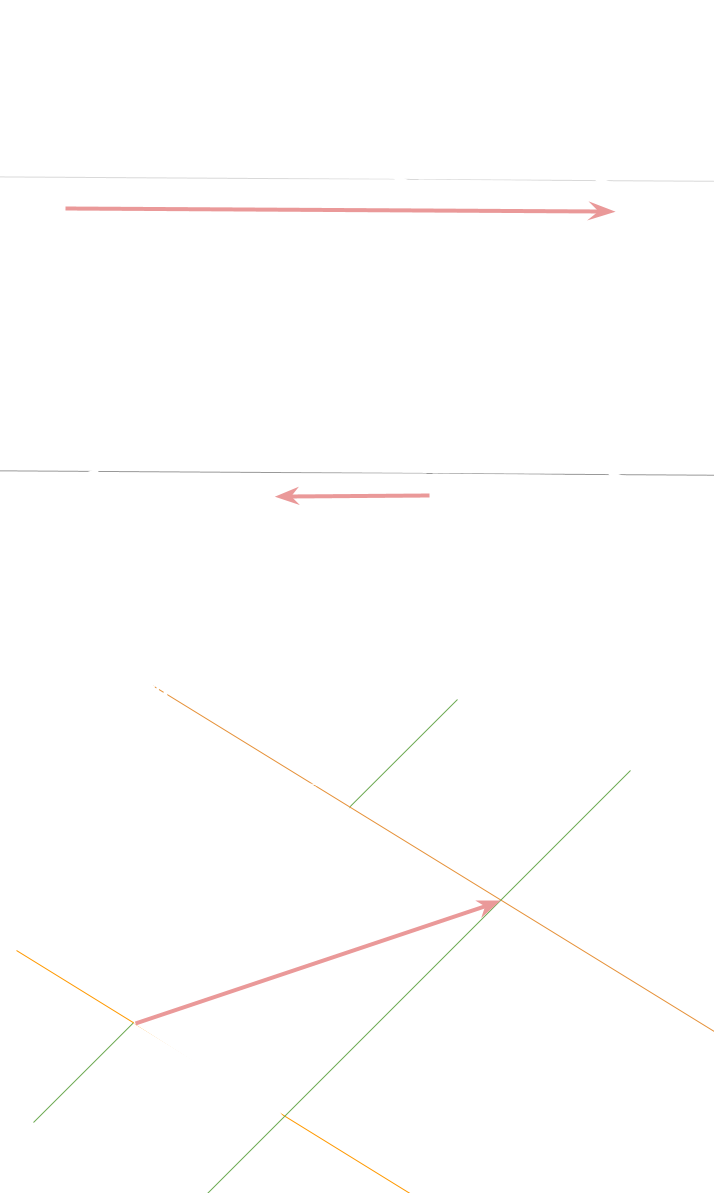
Somma - stessa direzione, stesso verso
Il modulo della Risultante è la somma dei moduli delle forze.
Il vettore risultante è la freccia che va dalla coda del primo vettore alla punta del secondo.
R = F1 + F2
Somma - stessa direzione, verso opposto
Il modulo della Risultante è la diffrenza dei moduli delle forze.
R = F1 - F2
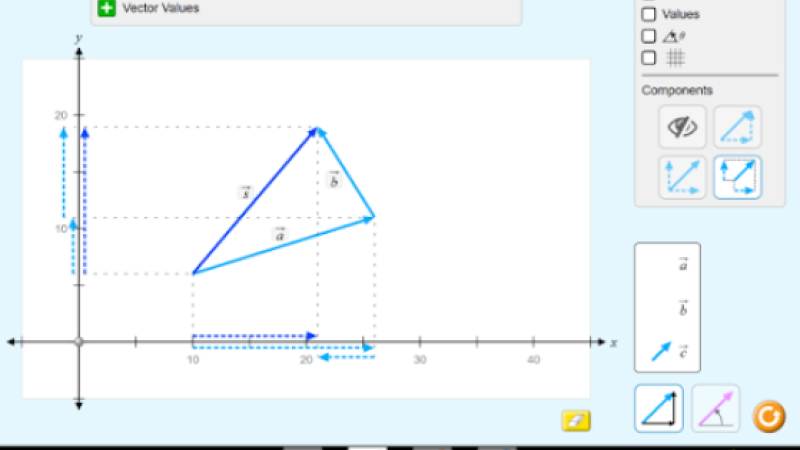
Somma - direzioni diverse
(metodo del parallelogramma)
Disegna i due vettori partendo dallo stesso punto.
Completa un parallelogramma usando i vettori come lati.
La risultante è la diagonale del parallelogramma.
Il calcolo matematico è possibile grazie alle applicazioni trigonometriche (seno e coseno), ma in questa fase basta disegnare bene le forze e musurare il risultato. In alcuni casi casi si può utilizzare la geometria base per calcolare le diagonali (con teorema di pitagora, triangoli equilateri, ecc).
Vettore per scalare
Simbologia
1) vettore "completo" 2) solo il modulo 3) grandezza scalare
$$ \overrightarrow{A} \sim | \overrightarrow{A} | \sim b $$
$$ \overrightarrow{A} \cdot b = | \overrightarrow{A} | \cdot b $$
Risultato: un vettore. In pratica moltiplico il modulo.
Applicazione: Calcolo della forza
$$ \overrightarrow{F} = m \cdot \overrightarrow{a} $$
Prodotto Scalare e prodotto vettoriale
Prodotto Scalare e Vettoriale li riprenderemo più avanti in modo semplificato, non saranno nei test.
Prodotto Scalare
$$ \overrightarrow{A} \cdot \overrightarrow{B} = | \overrightarrow{A} | \cdot | \overrightarrow{B} | \cdot cos(𝜃) $$
Risultato: uno scalare.
Applicazione: Calcolo del lavoro meccanico
$$ L = \overrightarrow{F} \cdot \overrightarrow{d} $$
Prodotto Vettoriale
$$ \overrightarrow{A} \times \overrightarrow{B} = | \overrightarrow{A} | \cdot | \overrightarrow{B} | \cdot sen(𝜃) $$
Risultato: un vettore ortogonale al piano dei due vettori.
Applicazione: Momento torcente
$$ \overrightarrow{M} = \overrightarrow{F} \times \overrightarrow{d} $$

Forze con stessa direzione, versi opposti... semplicemente vince chi ha più forza!.

Pala eolica: girano perché le eliche hanno un preciso angolo rispetto alla direzione (e verso) del vento (scomposizione delle forze).

La curva dipende da tanti vettori: velocità, equilibrio del corpo, forza delle gambe, attrito neve/lamine...
LEGGE DI ARCHIMEDE
Concetto
Un corpo immerso in un fluido riceve una spinta verso l'altro pari al peso del volume di fluido che sposta.
Questa forza che si oppone all'affondamento del corpo viene chiamata spinta di Archimede o in alternativa spinta idrostatica.
Quindi più è denso l'oggetto, più facilmente affonda.
Viceversa, più è denso il fluido, più rimane a galla.
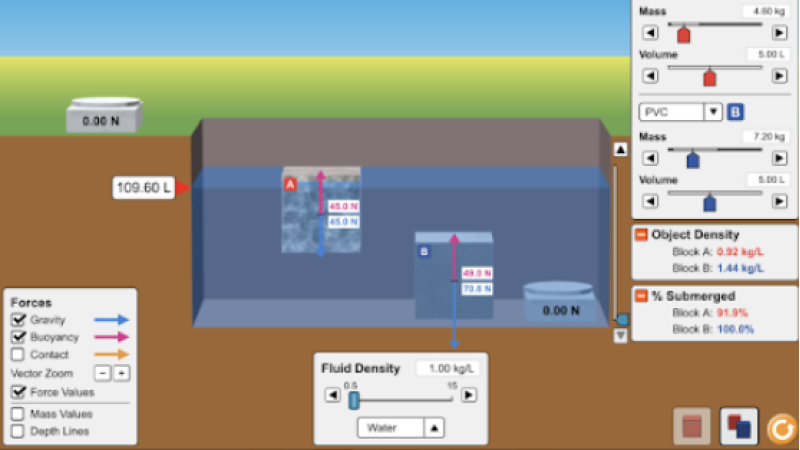
In questo capitolo non vengono esplicitate le formule, ma si mette a disposizione nei contenuti extra qui sotto un simulatore della forza di archimede.

Il Mar Morto ha un'alta concentrazione di sale (circa 10 volte più salato del Mar Mediterraneo). Questo lo rende più denso rispetto alla normale acqua (e rispetto ai nostri mari). Pertanto è molto più facile galleggiare!

L'acciaio è molto più denso dell'acqua, quindi affonda. Però se all'interno è cavo (riempito d'aria) il volume d'acqua spostato è molto più grande del volume totale di acciaio utilizzato per costruire la nave. Per questo le navi galleggiano.
CONTENUTI EXTRA
ESERCIZI

1
L'immagine rappresenta un palloncino riempito con elio legato ad una sedia. Schematizza l'immagine in figura e applica le forze a cui è soggetta. Dimostra quindi che il tutto rimane fermo.
2
Somma di Vettori. Un corpo è tirato da due forze:
- F1 = 12N verso est
- F2 = 16N verso nord
Determina il modulo, la direzione e il verso della forza risultante.
3
Un ragazzo su un pattino spinge contro un muro con una forza di F = 30N. Calcola la forza che il muro esercita sul ragazzo.
4
Un blocco di m = 5kg è spinto su una superficie con una forza di F = 20N. Se l’attrito oppone una forza di Fa = 5N, calcola l’accelerazione.
5
Due masse sono collegate da una fune e passano su una puleggia senza attrito.
- m1 = 3kg
- m2 = 5kg
Trova l’accelerazione del sistema.
6
Un blocco di 10kg è posto su un piano inclinato di 30°. Determina la componente della forza gravitazionale lungo il piano.
7
Una persona con m = 60 kg è in un ascensore che accelera verso l’alto a 2 m/s2. Calcola la forza che sopporta il pavimento dell'ascensore.
8
Un oggetto è lanciato verticalmente con F = 50N. Sapendo che la massa m = 2kg, calcola l’accelerazione iniziale.