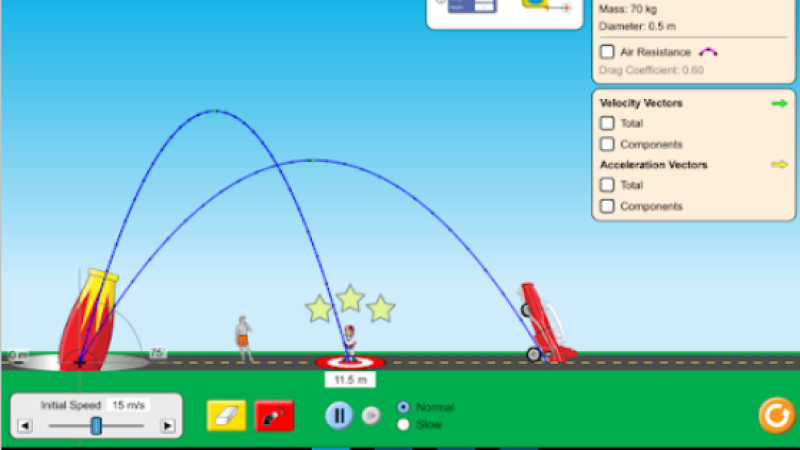
Cinematica
TEORIA CINEMATICA
CINEMATICA
Cos'è?
La cinematica studia il movimento dei corpi senza considerare le cause (forze) che lo determinano. Si concentra su grandezze come posizione, velocità, accelerazione e tempo.
Concetti
Moto
Descrizione del cambiamento di posizione di un corpo rispetto a un sistema di riferimento.
Sistema di riferimento
Punto o sistema rispetto al quale si misura il moto.
Esempio: Un’automobile rispetto alla strada.
Traiettoria
Linea descritta da un corpo in movimento.
Può essere rettilinea o curvilinea.
Grandezze
s > Posizione: la distanza di un corpo rispetto al sistema di riferimento.
Misurata in metri [m]
v > Velocità: la variazione della posizione nel tempo
Misurata in metri al secondo [m/s]
velocità media
$$ v = \frac{\Delta s}{\Delta t} $$
a > Accelerazione: la variazione della velocità nel tempo.
Misurata in metri al secondo quadrato [m/s2]
accelerazione media:
$$ a = \frac{\Delta v}{\Delta t} $$
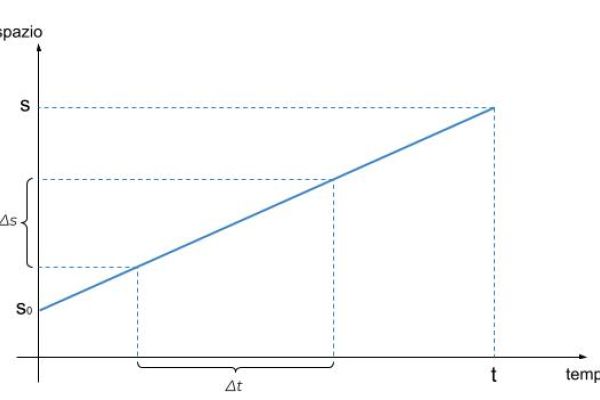
Visivamente i concetti cinematici sono esprimibili con dei grafici basati sullo scorrere del tempo...

Nell'ingegneria ferroviaria vengono usati modelli molto simili (opportunamente adattati) per definire gli orari ed evitare collisioni.

L'orbita di pianeti, satelliti (naturali e artificiali), missioni spaziali si avvicina molto alle semplificazioni della cinematica poiché le forze esterne come l'attrito che degradano il movimento "pulito" sono praticamente nulle.
TEORIA DEL MOTO
Moto rettilineo uniforme
Concetto
Il corpo si muove lungo una retta con velocità costante.
Equazioni del moto
Calcolare la posizione dopo un tot di tempo.
$$ s = s_0 + v\cdot t $$
Calcolare la velocità media.
$$ v = \frac{\Delta s}{\Delta t} $$
s > posizione finale
s0 > posizione iniziale
v > velocità costante
t > tempo
Δ > "delta" ovvero l'intervallo di spazio ( Δs ) e tempo ( Δt )
Grafico
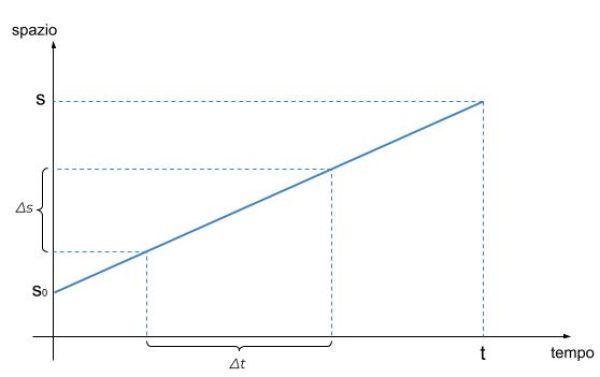
Moto uniformemente accelerato
Concetto
Il corpo si muove lungo una retta con accelerazione costante.
Equazioni del moto
Calcolare la velocità dopo un tot di tempo.
$$ v = v_0 + a\cdot t $$
Calcolare la posizione dopo un tot di tempo.
$$ s = s_0 + v_0\cdot t + \frac{1}{2}\cdot a\cdot t^2 $$
s > posizione finale
s0 > posizione iniziale
v > velocità finale
v0> velocità iniziale
a > accelerazione costante
t > tempo
t2 > tempo al quadrato
Grafici
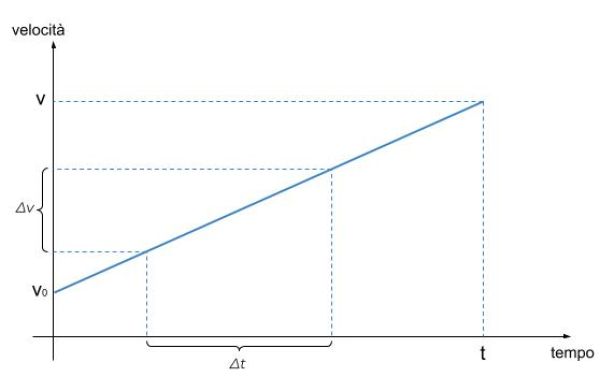
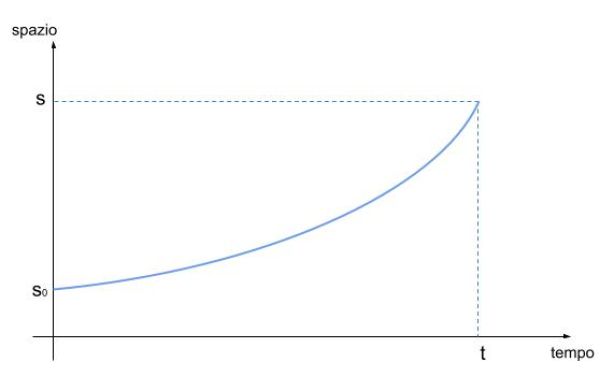
Moto circolare uniforme
Concetto
Il corpo si muove lungo una traiettoria circolare con velocità costante.
Equazioni del moto
Calcolare la velocità angolare.
$$ \omega = \frac{\Delta\theta}{\Delta t} $$
Calcolare la velocità tangenziale.
$$ v_t = \frac{2\pi r}{T} $$
Calcolare l'accelerazione centripeta:
$$ a_c = \frac{v^2}{r} $$
ω > velocità angolare
θ > angolo percorso
vt > velocità tangenziale (costante)
r > raggio della traiettoria
ac > accelerazione centripeta
t > tempo
T > periodo, ossia il tempo di un intero giro
Rappresentazione grafica
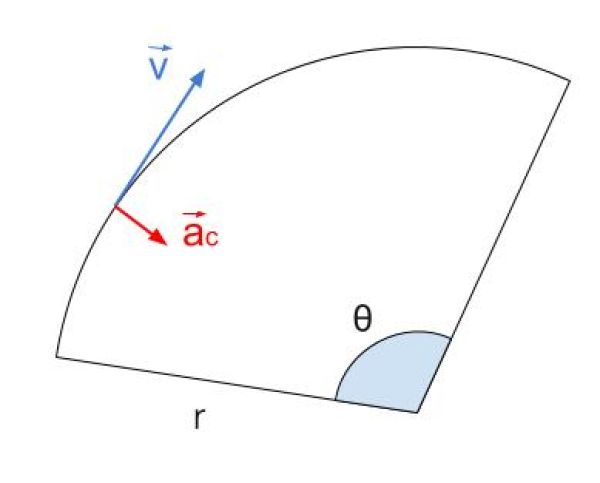
Osservazioni
Quando affronto una curva, si forma un'accelerazione centripeta che fà ruotare la velocità costante.
- Ricordando che secondo la seconda Legge di Newton F = m ⋅ a si sviluppa una Forza centripeta. Noi in macchina percepiamo una forza fittizia opposta: la forza centrifuga. Questo perché il nostro corpo vorrebbe andare per la sua strada (prima legge di Newton) ma la macchina ci fa modificare la nostra traiettoria.
- Quello che permette di fare la curva è l'attrito tra gomma e asfalto. Come visto in statica l'attrito statico ha un limite massimo ed è maggiore di quello dinamico. Quando Fc (forza centripeta) supera la Fs massima (forza di attrito statico massimo) la macchina comincia a slittare e diventa difficile riprenderla.
- Se noi affrontiamo la stessa curva (raggio uguale) a velocità tripla (x3), l'accelerazione sarà 9 volte superiore (varia al quadrato!).
- Se impprovvisamente viene a mancare la Forza di attrito (perché entro in una lastra di ghiaccio), anche la Forza centripeta sparisce (azione reazione - terza legge di Newton). Quindi la macchina continua con la stessa velocità nell'ultima direzione utlie... in pratica la macchina va dritta.

I piloti da pista o F1 devono percorrere la curva più velocemente possibile, ma senza superare la Forza di attrito (o forza centripeta) limite che permette alle gomme di rimanere in traiettoria. Alcuni arrivano al sovrasterzo (leggero e controllato slittamento gomme anteriori). L'importante è non andare in sottosterzo (slittano le ruote dietro) altrimenti vanno in testacoda...

Nel rally invece giocano superando il limite di Forza di attrito statica (o centripeta) limite facendo slittare le gomme posteriori (sottosterzo) anche grazie al gioco freno-acceleratore. Questo permette di fare curve molto strette riducendo il minimo i tempi di decelerazione a accelerazione. Devono stare molto attenti invece a non andare in sovrasterzo (slittamento gomme anteriori) che li porta fuori strada.

L'accelerazione di qualsiasi natura influisce sul nostro corpo e la nostra percezione. Quando il nostro cervello non prevede o comprende perché sta succedendo questo cambiamento la risposta naturale è la nausea.
Quindi per chi è soggetto a nausea in auto, meglio guardare la strada avanti a sè, sedere davanti, NON GUARDARE IL TELEFONO!!
CONTENUTI EXTRA
ESERCIZI